Les mathématiques sont omniprésentes. Tout ou presque est fait à base de mathématiques, notamment les programmes informatiques, les routes, les habitations, les calculs financiers, les transactions, et bien d’autres choses encore.
On ne s’en rend pas forcément compte, on a tendance à trouver cela abstrait, futile, trop difficile, et tant d’autres adjectifs péjoratifs, mais les mathématiques sont là pour nous faciliter la vie.
On reconnaît plusieurs techniques mathématiques utilisées dans la vie quotidienne, notamment les matrices. Ces dernières sont très utilisées en informatique, en architecture, mais également en infographie.
Les opérations sur les matrices sont nombreuses et variées, parmi elles le calcul du déterminant qu’on vous explique à travers cet article.
Le monde des matrices
Les matrices sont des tableaux de nombres qui servent à interpréter divers phénomènes linéaires. Par ailleurs, leur utilisation se fait dans énormément de domaines.
Ils facilitent en effet grandement l’analyse des résultats, et diverses techniques sont employés dans ce but, notamment la méthode de Gauss et ses différentes variantes (notamment la méthode de Gauss-Seidel), ou la méthode LU, la méthode de Jacobi, etc.
Les matrices sont utilisées en analyse numérique, en graphisme, en génie civil et en architecture, et même dans d’autres branches de l’ingénierie telles que la mécanique.
Calculer le déterminant d’une matrice 3 x 3
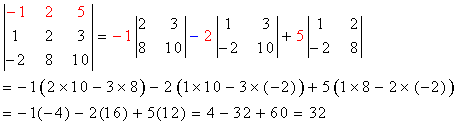
Nous vous apprenons à travers cet article à calculer le déterminant d’une matrice carrée (soit ayant le même nombre de lignes et de colonnes) 3 x 3 (avec trois lignes et trois colonnes !).
N’hésitez pas à bien suivre l’exemple ci-dessous et de l’appliquer sur une matrice carrée 3 x 3 de votre choix.
- Commencez par inscrire votre matrice sur un bout de papier. N’oubliez pas de choisir une matrice 3 x 3.
- Prenez une ligne ou une colonne quelconque qui sera votre ligne (ou colonne) de référence pour la suite des opérations.
- Barrez toutes les lignes et les colonnes du premier coefficient de votre ligne ou colonne choisie.
- Commencez par calculer le déterminant de la matrice restante (qui sera forcément une matrice carrée 2 x 2) en multipliant et soustrayant les coefficients opposés.
- Multipliez le nombre choisi par le coefficient de la ligne ou colonne choisie.
- Déterminez le signe du nombre résultant qui sera soit positif, soit négatif.
- Poursuivez avec les autres coefficients de la ligne ou de la colonne choisie en répétant les précédentes opérations.
- Au final, additionnez les trois nombres, et déterminez ainsi le déterminant de votre matrice 3 x 3.
Sachez qu’il existe d’autres méthodes pour le calcul d’un déterminant, celle-ci étant jugée plus facile. Petite astuce : si les coefficients d’une ligne (ou colonne) sont tous égaux à zéro, alors le déterminant est directement mis à zéro.
Bien entendu, vous pouvez utiliser cette méthode pour le calcul du déterminant de n’importe quelle matrice (4 x 4, 5 x 5, et plus !). L’opération sera simplement plus longue à réaliser.